2 Point Pattern data

Learning goals

Understand spatial data structures used in R
Understand what a point pattern and a point process is
Understand what an observation window is
Get familiar with the tools used in point pattern data analysis
See the alignment with MaxEnt

Reading materials

From Spatial Data Science: with applications in R:

Chapter 11: Point Patterns
Chapter 7: sf and stars

Summary

Intro to sf and stars
Intro to spatstat
Point patterns, density functions
Interactions in point processes
Simulating point process
Modelling density as a function of external variables

2.1 Intro to `sf` and `stars`

Briefly: sf provides classes and methods for simple features
- a feature is a “thing”, with geometrical properties (point(s), line(s), polygon(s)) and attributes
- sf stores data in data.frames with a list-column (of class sfc) that holds the geometries

the Simple Feature standard

“Simple Feature Access” is an open standard for data with vector geometries. It defines a set of classes for geometries and operations on them.

“simple” refers to curves that are “simply” represented by points connected by straight lines
connecting lines are not allowed to self-intersect
polygons can have holes, and have validity constraints: holes cannot extrude the outer ring etc.
All spatial software uses this: ArcGIS, QGIS, PostGIS, other spatial databases, …

Why do all functions in `sf` start with `st_`?

see here

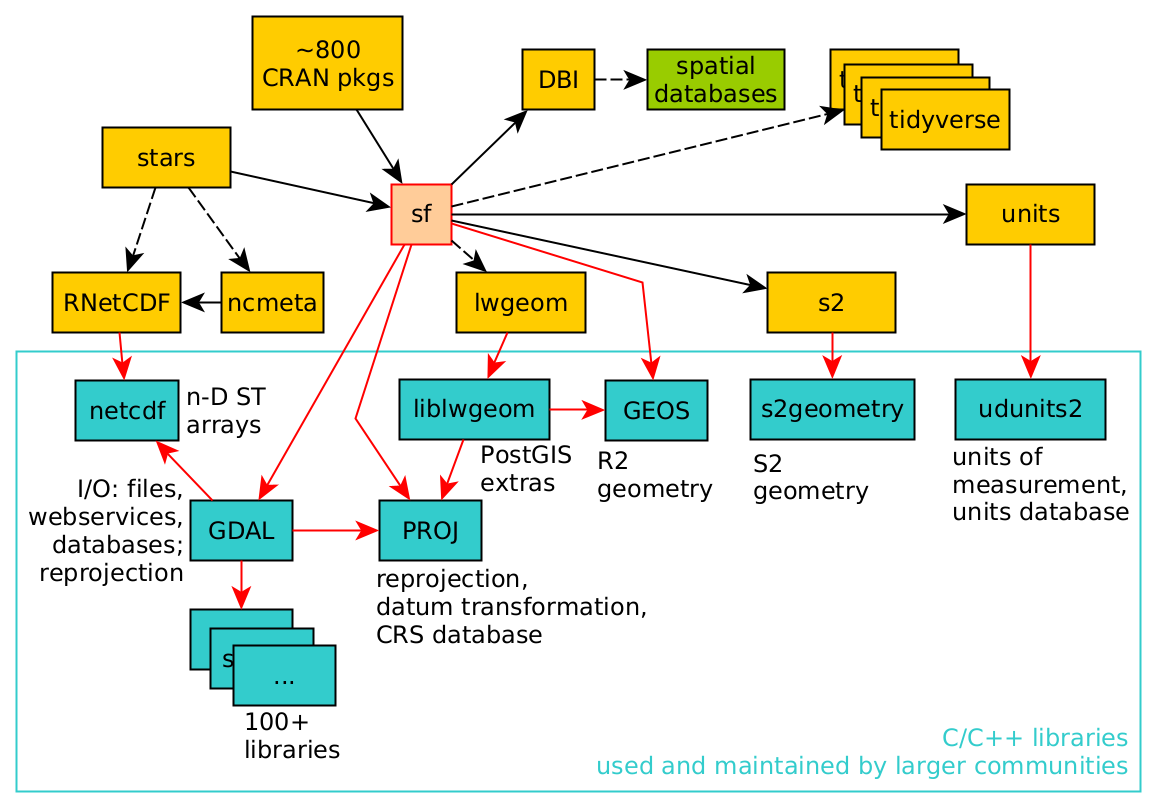
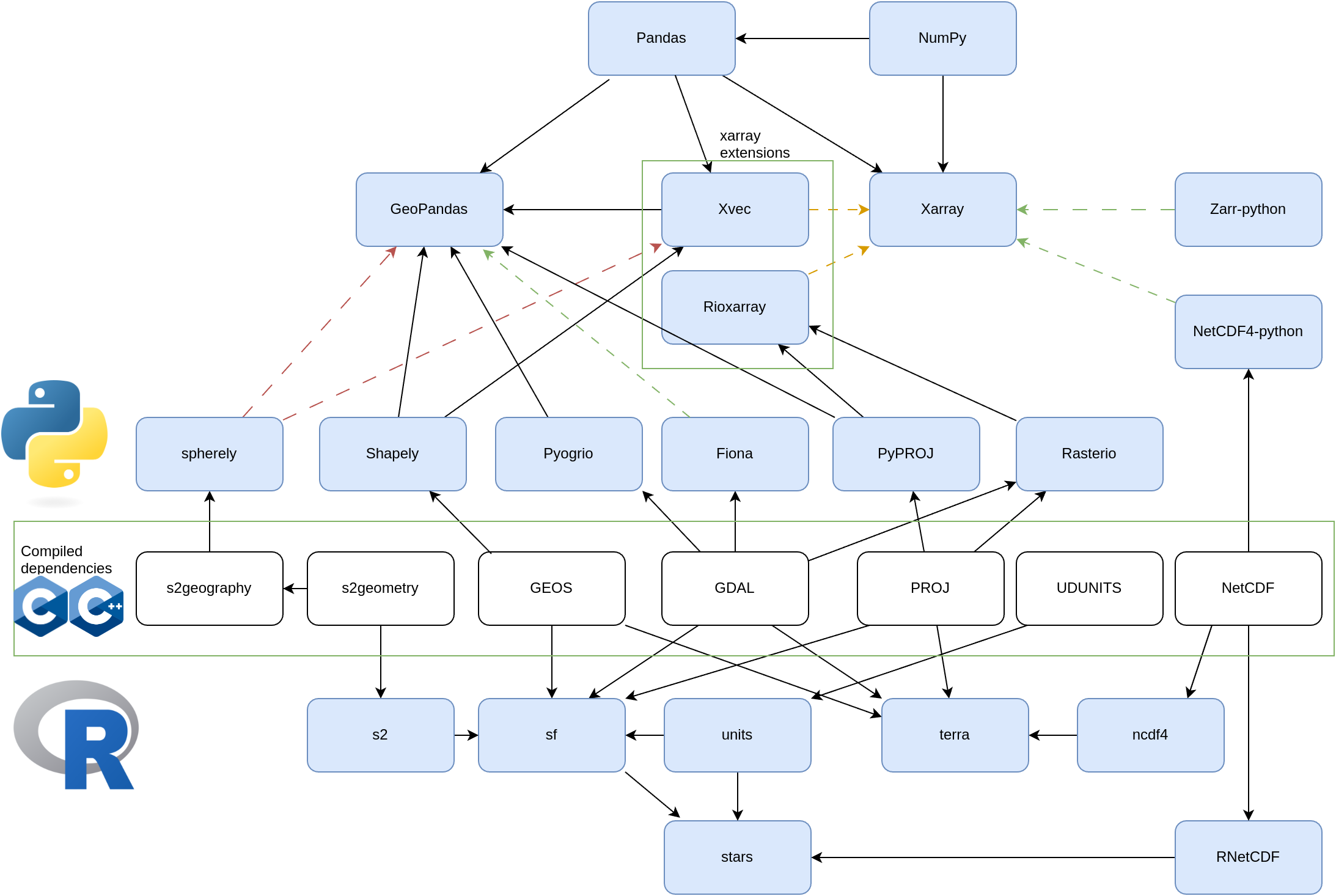
The larger geospatial open source ecosystem

R and beyond:

Figure 2.1: sf and its dependencies; arrows indicate strong dependency, dashed arrows weak dependency

Figure 2.2: upstream dependencies on OSGEO and other C/C++ libraries in R and Python spatial data sciece packages

`sf` operators, how to understand?

sf has objects at three nested “levels”:

sfg: a single geometry (without coordinate reference system)
sfc: a set of sfg geometries, with a coordinate reference system and bounding box
sf: a data.frame or tibble with at least one geometry (sfc) column
Operations not involving geometry (data.frame; base R; tidyverse)
- geometry column + sf class is sticky!
- this can be convenient, and sometimes annoying
- use as.data.frame or as_tibble to strip the sf class label
Operations involving only geometry
- predicates (resulting TRUE/FALSE)
  - unary
  - binary: DE9-IM; work on two sets, result sgbp, which is a sparse logical matrix representation
    - is_within_distance
- measures
  - unary: length, area
  - binary: distance, by_element = FALSE
- transformers
  - unary: buffer, centroid
  - binary: intersection, union, difference, symdifference
  - n-ary: intersection, difference
Operations involving geometry and attributes
- many of the above!
- st_join
- aggregate
- st_interpolate_aw: requires expression whether variable is spatially extensive or intensive

2.2 `sf` and `spatstat`

We can try to convert an sf object to a ppp (point pattern object in spatstat):

library(sf)
# Linking to GEOS 3.12.1, GDAL 3.8.4, PROJ 9.4.0; sf_use_s2() is TRUE
library(spatstat)
# Loading required package: spatstat.data
# Loading required package: spatstat.univar
# spatstat.univar 3.0-1
# Loading required package: spatstat.geom
# spatstat.geom 3.3-3
# Loading required package: spatstat.random
# spatstat.random 3.3-2
# Loading required package: spatstat.explore
# Loading required package: nlme
# spatstat.explore 3.3-2
# Loading required package: spatstat.model
# Loading required package: rpart
# spatstat.model 3.3-2
# Loading required package: spatstat.linnet
# spatstat.linnet 3.2-2
# 
# spatstat 3.2-1 
# For an introduction to spatstat, type 'beginner'
demo(nc, echo = FALSE, ask = FALSE)
pts = st_centroid(st_geometry(nc))
as.ppp(pts) # ???
# Error: Only projected coordinates may be converted to spatstat
# class objects

Note that sf interprets a NA CRS as: flat, projected (Cartesian) space.

Why is this important?

(p1 = st_point(c(0, 0)))
# POINT (0 0)
(p2 = st_point(c(1, 0)))
# POINT (1 0)
st_distance(p1, p2)
#      [,1]
# [1,]    1
st_sfc(p1, crs = 'OGC:CRS84')
# Geometry set for 1 feature 
# Geometry type: POINT
# Dimension:     XY
# Bounding box:  xmin: 0 ymin: 0 xmax: 0 ymax: 0
# Geodetic CRS:  WGS 84 (CRS84)
# POINT (0 0)
st_distance(st_sfc(p1, crs = 'OGC:CRS84'), st_sfc(p2, crs = 'OGC:CRS84'))
# Units: [m]
#        [,1]
# [1,] 111195
(p1 = st_point(c(0, 80)))
# POINT (0 80)
(p2 = st_point(c(1, 80)))
# POINT (1 80)
st_distance(p1, p2)
#      [,1]
# [1,]    1
st_distance(st_sfc(p1, crs = 'OGC:CRS84'), st_sfc(p2, crs = 'OGC:CRS84'))
# Units: [m]
#       [,1]
# [1,] 19309

Also areas:

p = st_as_sfc("POLYGON((0 80, 120 80, 240 80, 0 80))")
st_area(p)
# [1] 0
st_area(st_sfc(p, crs = 'OGC:CRS84')) |> units::set_units(km^2)
# 1620544 [km^2]
pole = st_as_sfc("POINT(0 90)")
st_intersects(pole, p)
# Sparse geometry binary predicate list of length 1, where the
# predicate was `intersects'
#  1: (empty)
st_intersects(st_sfc(pole, crs = 'OGC:CRS84'), st_sfc(p, crs = 'OGC:CRS84'))
# Sparse geometry binary predicate list of length 1, where the
# predicate was `intersects'
#  1: 1

What to do with nc? Project to \(R^2\) (flat space):

nc |> st_transform('EPSG:32119') |> st_centroid() -> pts
# Warning: st_centroid assumes attributes are constant over
# geometries
pts
# Simple feature collection with 100 features and 14 fields
# Attribute-geometry relationships: constant (6), aggregate (8)
# Geometry type: POINT
# Dimension:     XY
# Bounding box:  xmin: 149000 ymin: 36500 xmax: 898000 ymax: 306000
# Projected CRS: NAD83 / North Carolina
# First 10 features:
#     AREA PERIMETER CNTY_ CNTY_ID        NAME  FIPS FIPSNO CRESS_ID
# 1  0.114      1.44  1825    1825        Ashe 37009  37009        5
# 2  0.061      1.23  1827    1827   Alleghany 37005  37005        3
# 3  0.143      1.63  1828    1828       Surry 37171  37171       86
# 4  0.070      2.97  1831    1831   Currituck 37053  37053       27
# 5  0.153      2.21  1832    1832 Northampton 37131  37131       66
# 6  0.097      1.67  1833    1833    Hertford 37091  37091       46
# 7  0.062      1.55  1834    1834      Camden 37029  37029       15
# 8  0.091      1.28  1835    1835       Gates 37073  37073       37
# 9  0.118      1.42  1836    1836      Warren 37185  37185       93
# 10 0.124      1.43  1837    1837      Stokes 37169  37169       85
#    BIR74 SID74 NWBIR74 BIR79 SID79 NWBIR79                  geom
# 1   1091     1      10  1364     0      19  POINT (385605 3e+05)
# 2    487     0      10   542     3      12 POINT (419198 306144)
# 3   3188     5     208  3616     6     260 POINT (458418 296669)
# 4    508     1     123   830     2     145 POINT (876266 298782)
# 5   1421     9    1066  1606     3    1197 POINT (752184 297618)
# 6   1452     7     954  1838     5    1237 POINT (789602 291533)
# 7    286     0     115   350     2     139 POINT (857738 297588)
# 8    420     0     254   594     2     371 POINT (815437 301289)
# 9    968     4     748  1190     2     844 POINT (689435 294013)
# 10  1612     1     160  2038     5     176 POINT (498892 294730)
(pp = as.ppp(pts))
# Marked planar point pattern: 100 points
# Mark variables: 
#    AREA PERIMETER CNTY_ CNTY_ID NAME FIPS FIPSNO CRESS_ID BIR74 
# SID74 NWBIR74 BIR79 SID79 NWBIR79
# window: rectangle = [148701, 898181] x [36519, 306144] units
st_as_sf(pp)
# Simple feature collection with 101 features and 15 fields
# Geometry type: GEOMETRY
# Dimension:     XY
# Bounding box:  xmin: 149000 ymin: 36500 xmax: 898000 ymax: 306000
# CRS:           NA
# First 10 features:
#     AREA PERIMETER CNTY_ CNTY_ID        NAME  FIPS FIPSNO CRESS_ID
# NA    NA        NA    NA      NA        <NA>  <NA>     NA       NA
# 1  0.114      1.44  1825    1825        Ashe 37009  37009        5
# 2  0.061      1.23  1827    1827   Alleghany 37005  37005        3
# 3  0.143      1.63  1828    1828       Surry 37171  37171       86
# 4  0.070      2.97  1831    1831   Currituck 37053  37053       27
# 5  0.153      2.21  1832    1832 Northampton 37131  37131       66
# 6  0.097      1.67  1833    1833    Hertford 37091  37091       46
# 7  0.062      1.55  1834    1834      Camden 37029  37029       15
# 8  0.091      1.28  1835    1835       Gates 37073  37073       37
# 9  0.118      1.42  1836    1836      Warren 37185  37185       93
#    BIR74 SID74 NWBIR74 BIR79 SID79 NWBIR79  label
# NA    NA    NA      NA    NA    NA      NA window
# 1   1091     1      10  1364     0      19  point
# 2    487     0      10   542     3      12  point
# 3   3188     5     208  3616     6     260  point
# 4    508     1     123   830     2     145  point
# 5   1421     9    1066  1606     3    1197  point
# 6   1452     7     954  1838     5    1237  point
# 7    286     0     115   350     2     139  point
# 8    420     0     254   594     2     371  point
# 9    968     4     748  1190     2     844  point
#                              geom
# NA POLYGON ((148701 36519, 898...
# 1            POINT (385605 3e+05)
# 2           POINT (419198 306144)
# 3           POINT (458418 296669)
# 4           POINT (876266 298782)
# 5           POINT (752184 297618)
# 6           POINT (789602 291533)
# 7           POINT (857738 297588)
# 8           POINT (815437 301289)
# 9           POINT (689435 294013)

2.3 Exercises

Compute the distance between POINT(10 -90) and POINT(50 -90), assuming (i) these are coordinates in a Cartesian space, and (ii) these are geodetic coordinates. What are the units of the result?
Load the nc dataset into your session (e.g. using library(sf); demo(nc)) and convert it into a stars object using (i) st_as_stars(), (ii) st_rasterize(), (iii) st_interpolate_aw()
Load the L7_ETMs dataset into your session (e.g. using library(stars); L7_ETMs = st_as_stars(L7_ETMs)), and convert the object to an sf object (i) using st_as_sf(), (ii) using st_as_sf(..., as_points = TRUE), and explain the differences (also plot the resulting sf objects). Randomly sample 100 points from the bounding box of L7_ETMs, and extract the image values at these points using st_extract(), and convert the result into an sf object.

2.4 Intro to `spatstat`

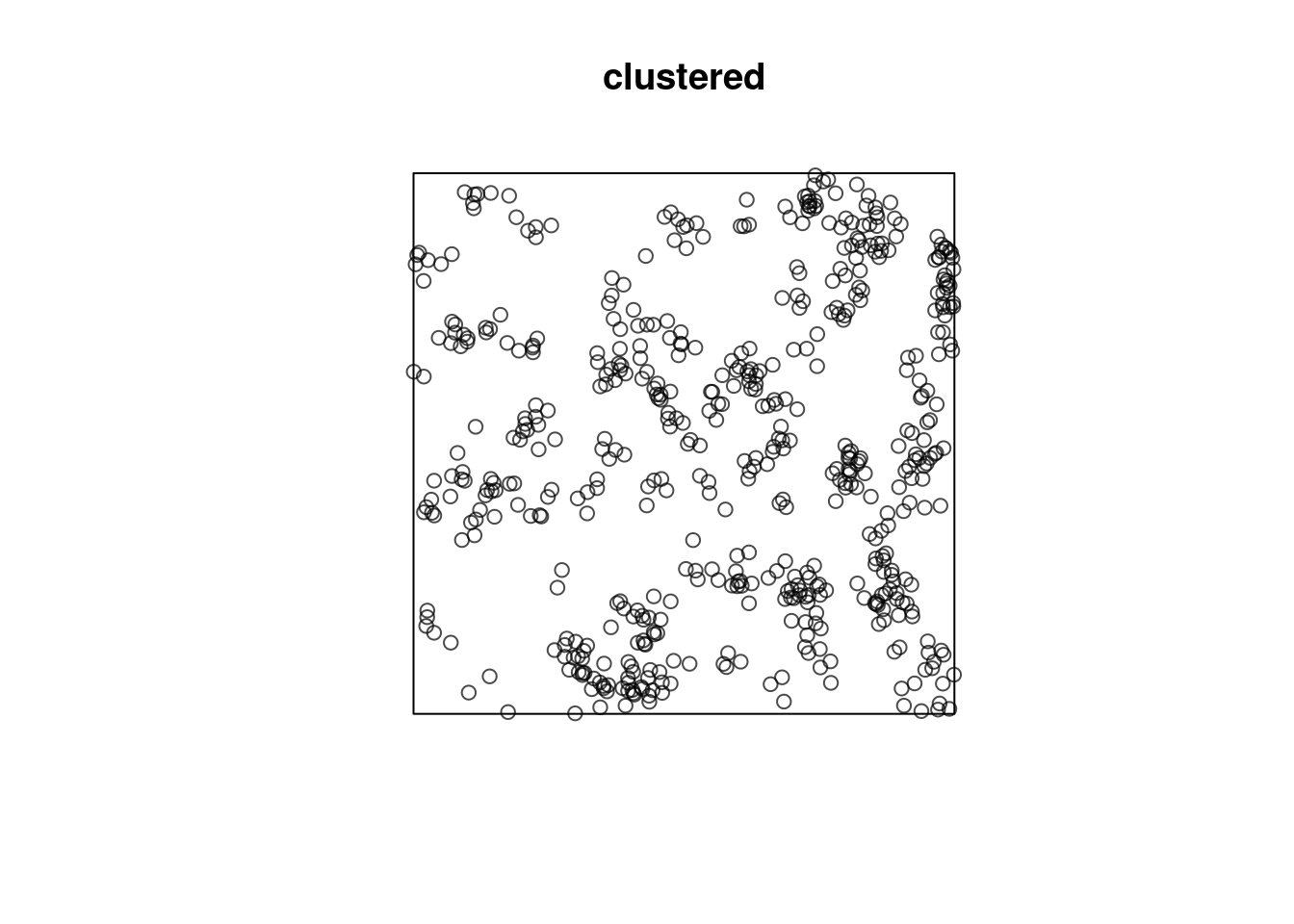
Consider a point pattern that consist of

a set of known coordinates
an observation window

We can ask ourselves: our point pattern be a realisation of a completely spatially random (CSR) process? A CSR process has

a spatially constant intensity (mean: first order property)
completely independent locations (interactions: second order property)

e.g.

library(spatstat)
set.seed(13431)
CSR = rpoispp(100)
plot(CSR)

Or does it have a non-constant intensity, but otherwise independent points?

ppi = rpoispp(function(x,y,...) 500 * x)
plot(ppi, main = "inhomogeneous")

Or does it have constant intensity, but dependent points:

cl <- rThomas(100, .02, 5)
plot(cl, main = "clustered")

hc <- rHardcore(0.05,1.5,square(50)) 
plot(hc, main = "inhibition")

or a combination:

#ff <- function(x,y) { 4 * exp(2 * abs(x) - 1) }
ff <- function(x,y) 10 * x
Z <- as.im(ff, owin())
Y <- rMatClust(10, 0.05, Z)
plot(Y)

2.5 Checking homogeneity

(q = quadrat.test(CSR))
# Warning: Some expected counts are small; chi^2 approximation may be
# inaccurate
# 
#   Chi-squared test of CSR using quadrat counts
# 
# data:  CSR
# X2 = 25, df = 24, p-value = 0.9
# alternative hypothesis: two.sided
# 
# Quadrats: 5 by 5 grid of tiles
plot(q)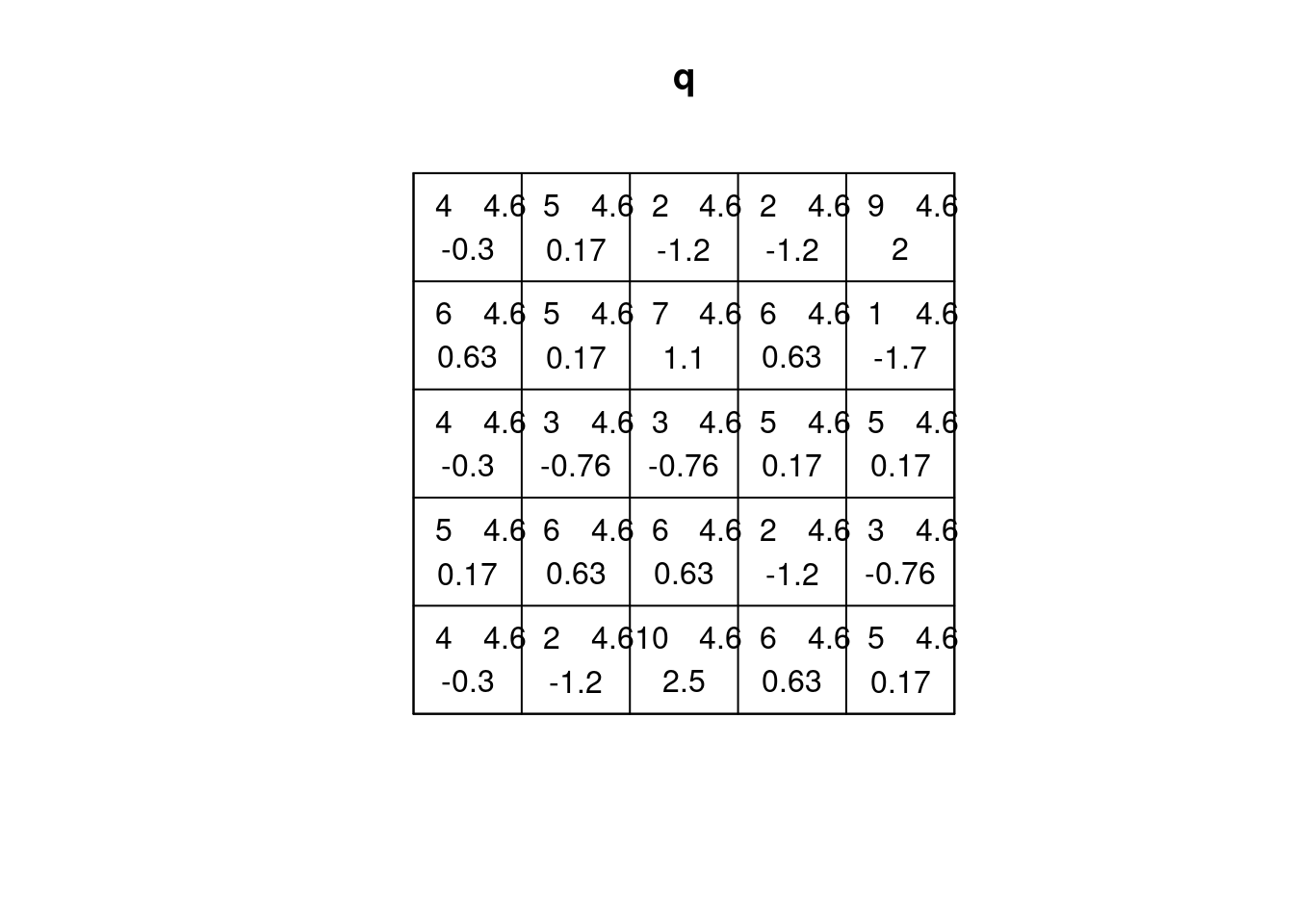

(q = quadrat.test(ppi))
# 
#   Chi-squared test of CSR using quadrat counts
# 
# data:  ppi
# X2 = 81, df = 24, p-value = 8e-08
# alternative hypothesis: two.sided
# 
# Quadrats: 5 by 5 grid of tiles
plot(q)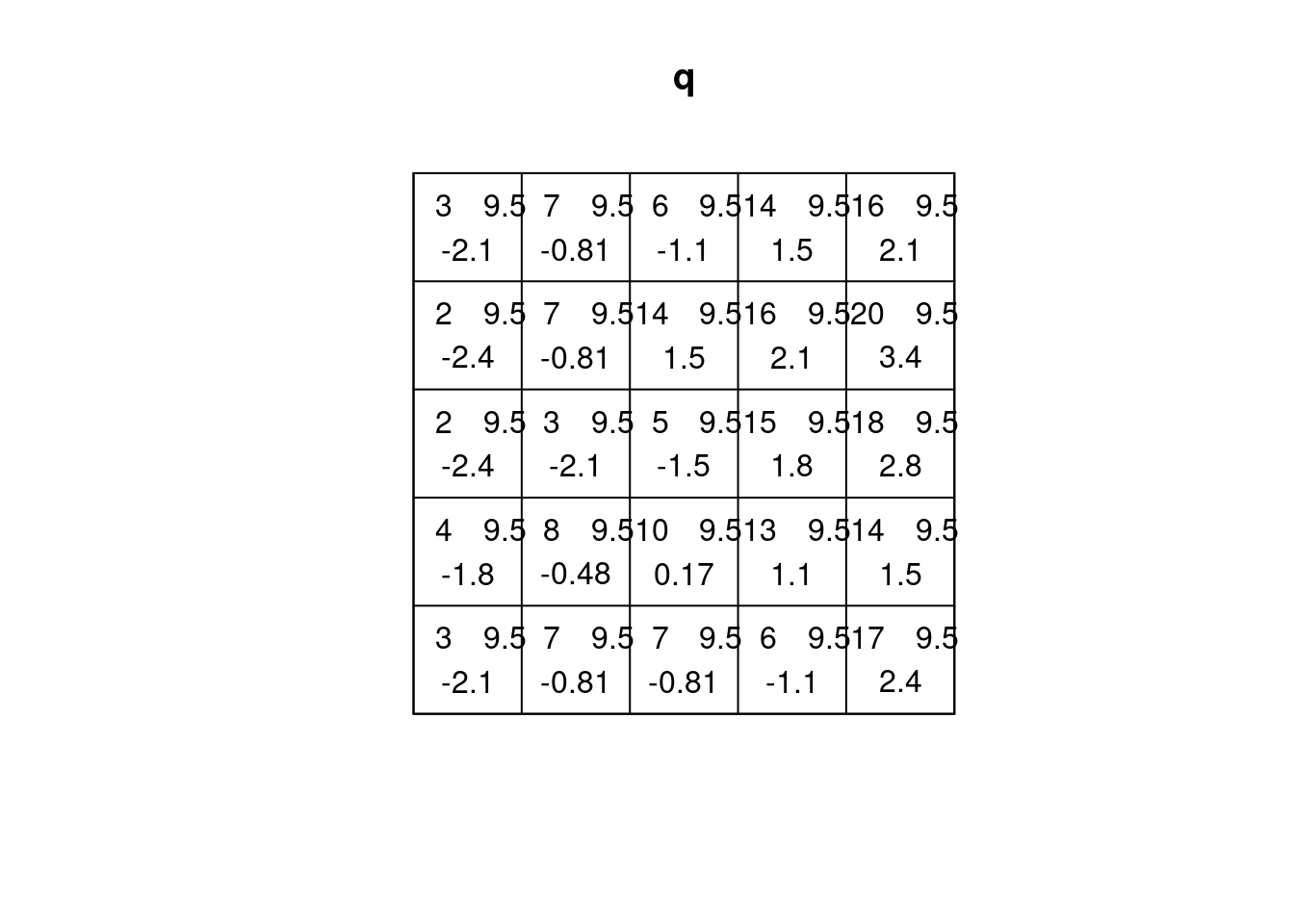

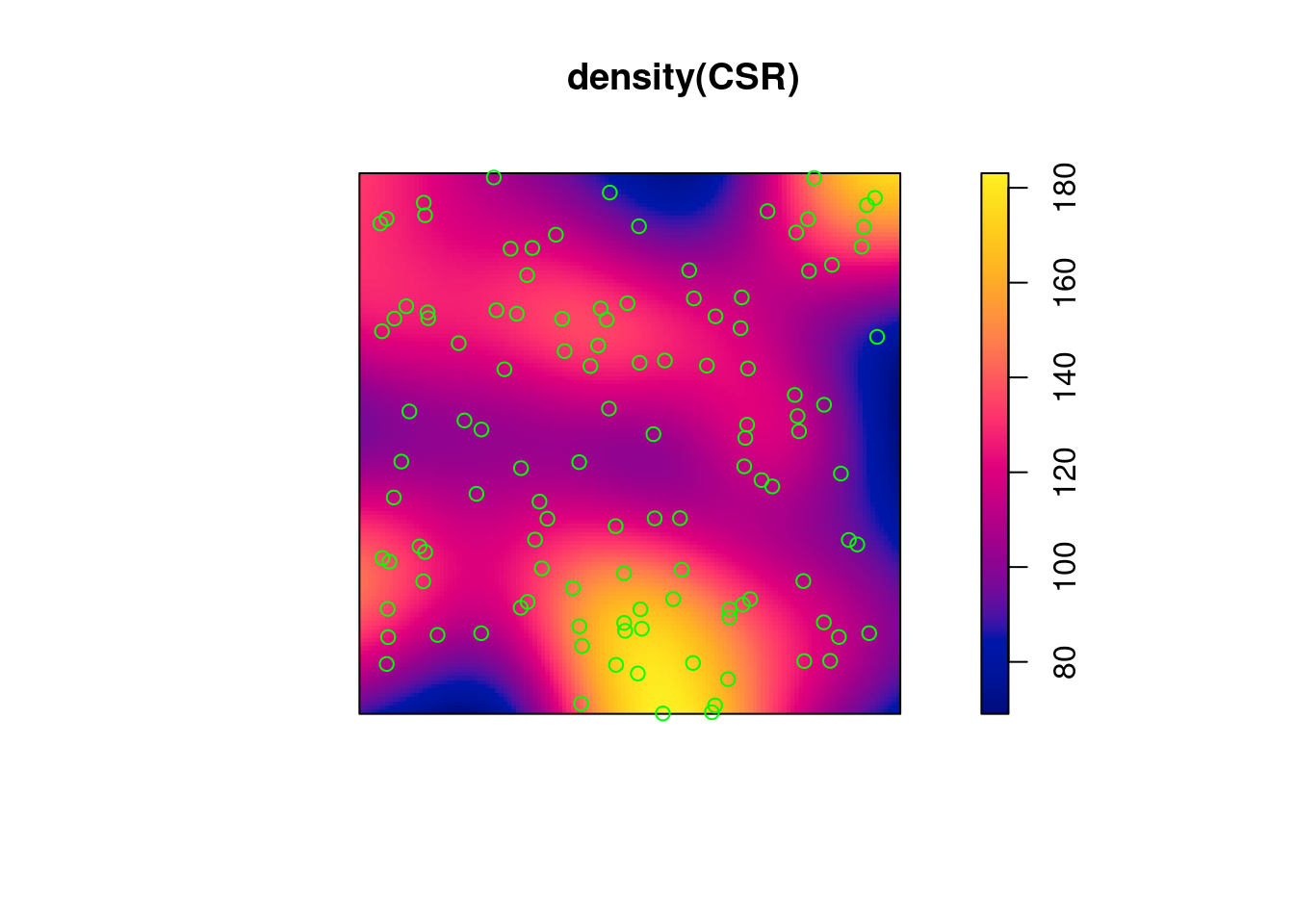
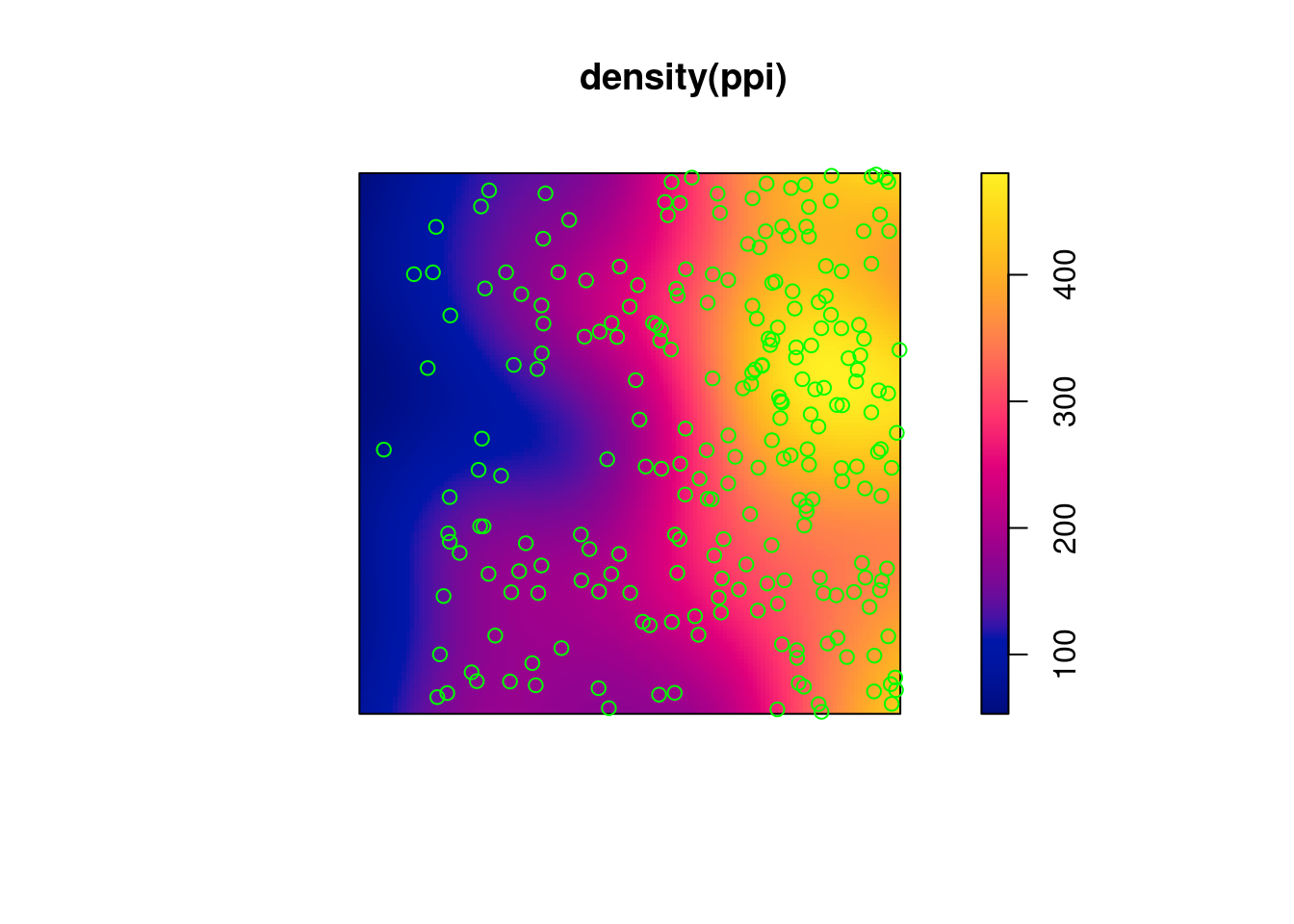
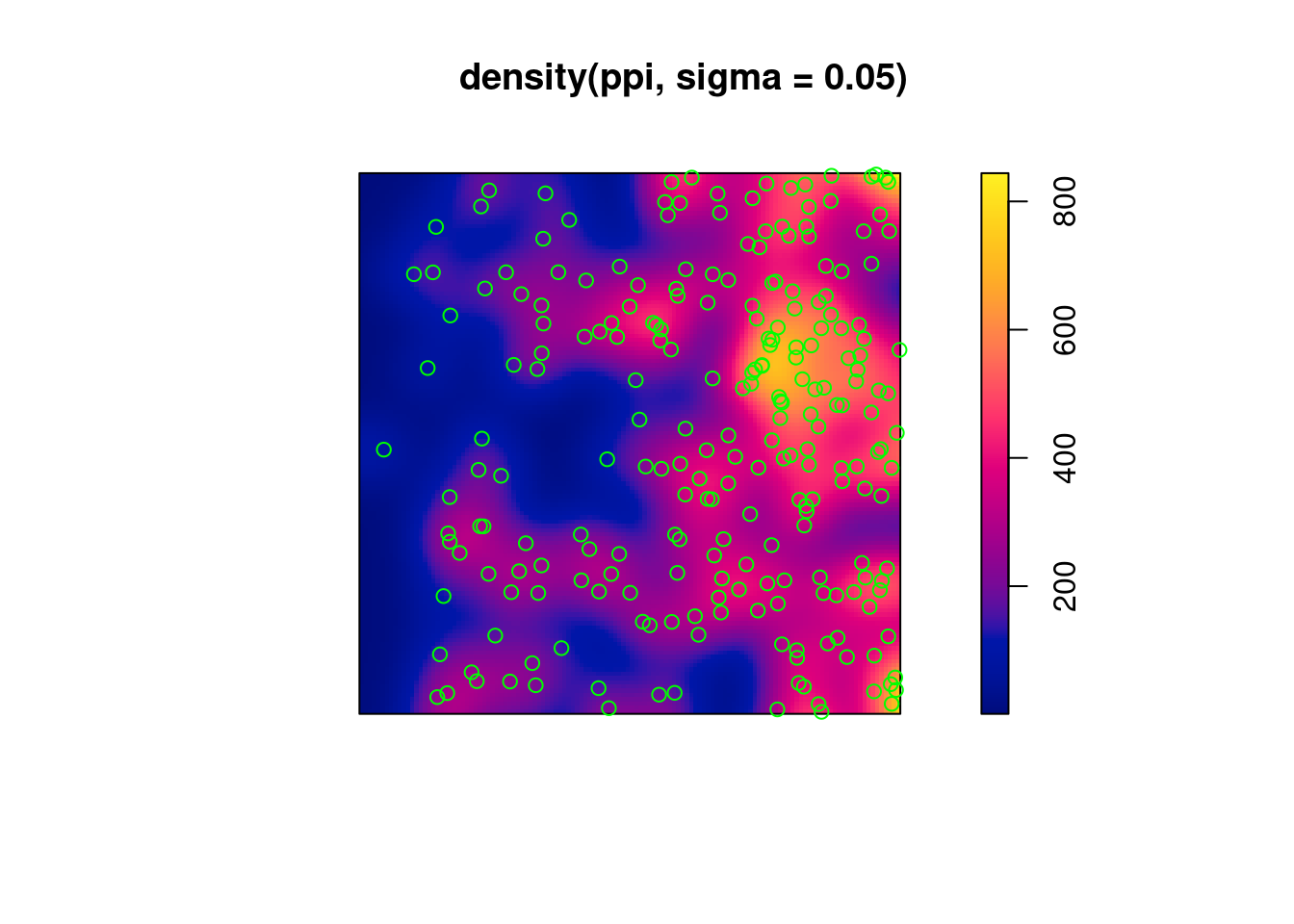
2.6 Estimating density

main parameter: bandwidth (sigma): determines the amound of smoothing.
if sigma is not specified: uses bw.diggle, an automatically tuned bandwidth

Correction for edge effect?

density(CSR) |> plot()
plot(CSR, add = TRUE, col = 'green')

density(ppi) |> plot()
plot(ppi, add = TRUE, col = 'green')

density(ppi, sigma = .05) |> plot()
plot(ppi, add = TRUE, col = 'green')

2.7 Assessing interactions: clustering/inhibition

The K-function (“Ripley’s K”) is the expected number of additional random (CSR) points within a distance r of a typical random point in the observation window.

The G-function (nearest neighbour distance distribution) is the cumulative distribution function G of the distance from a typical random point of X to the nearest other point of X.

envelope(CSR, Lest) |> plot()
# Generating 99 simulations of CSR  ...
# 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
# 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
# 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
# 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68,
# 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85,
# 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 
# 99.
# 
# Done.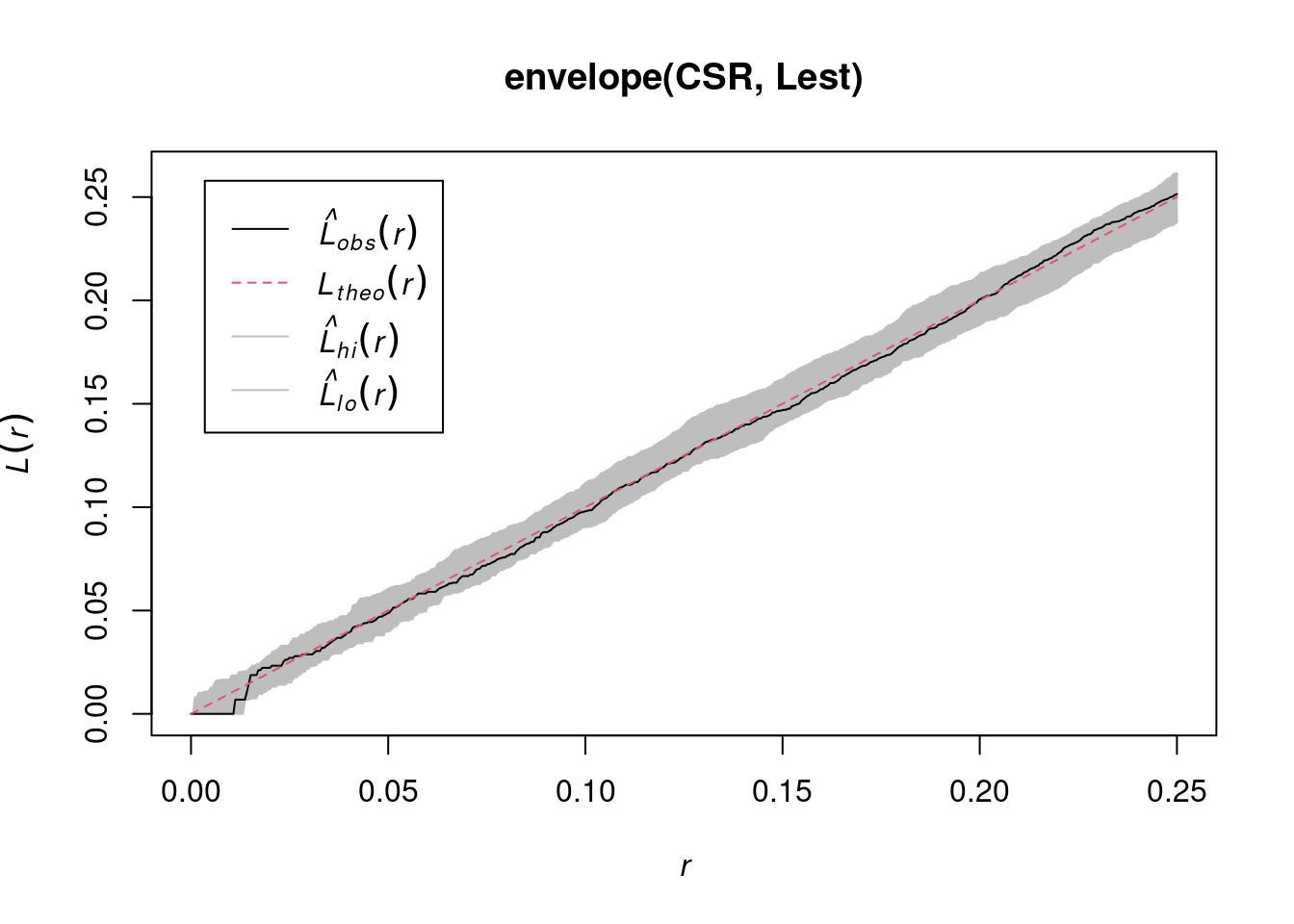

envelope(cl, Lest) |> plot()
# Generating 99 simulations of CSR  ...
# 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
# 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
# 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
# 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68,
# 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85,
# 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 
# 99.
# 
# Done.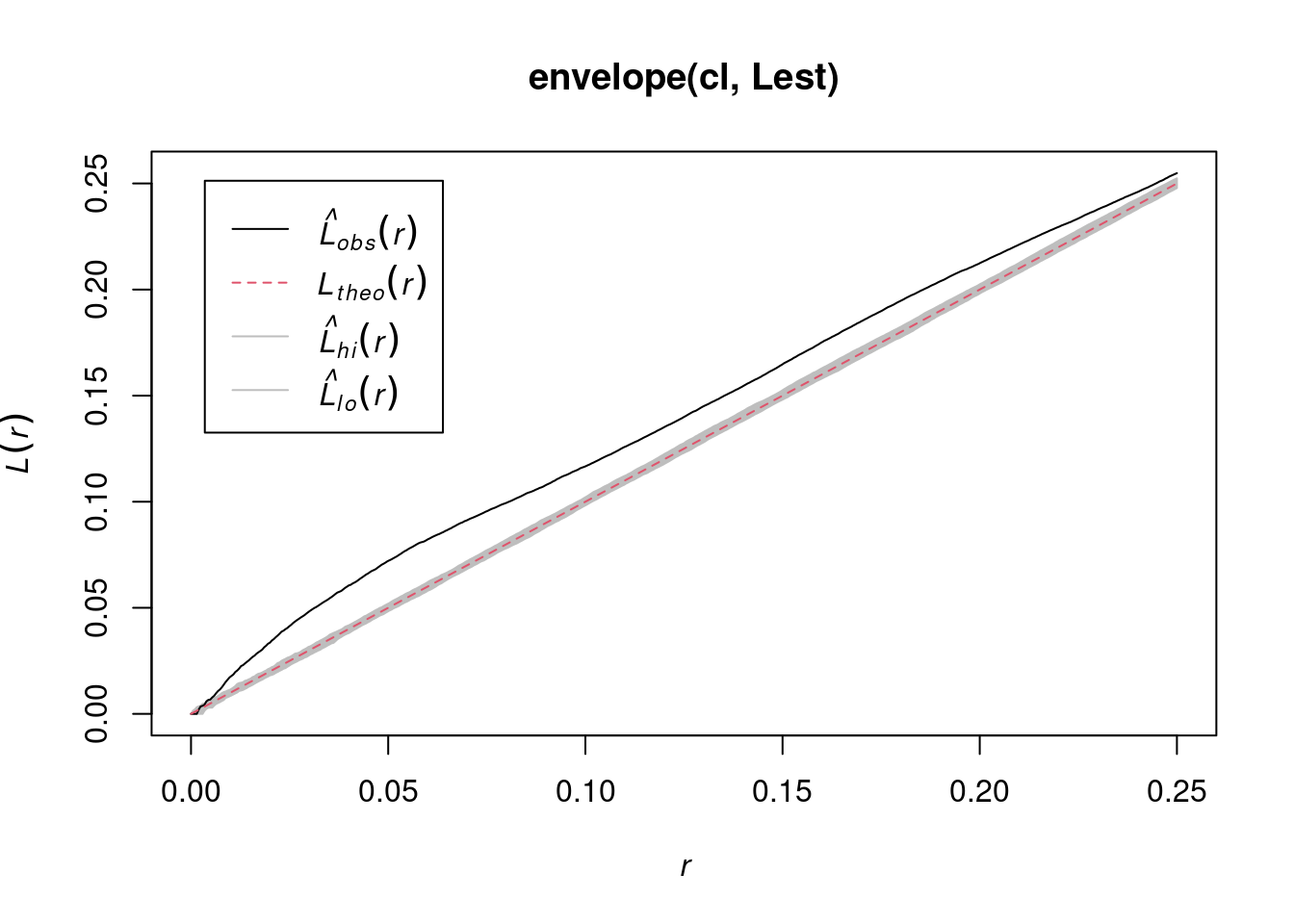

envelope(hc, Lest) |> plot()
# Generating 99 simulations of CSR  ...
# 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
# 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
# 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
# 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68,
# 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85,
# 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 
# 99.
# 
# Done.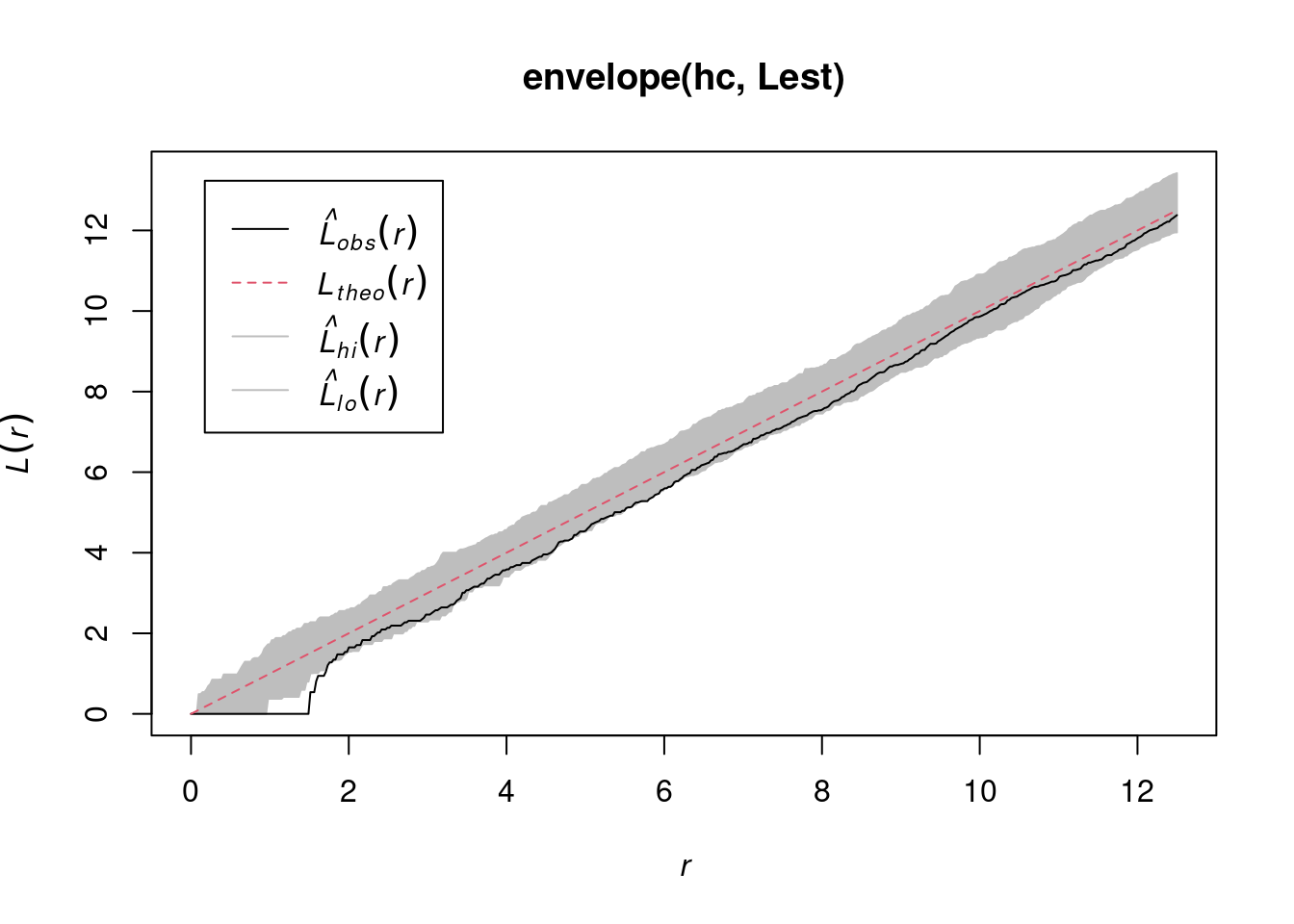

envelope(ppi, Lest) |> plot()
# Generating 99 simulations of CSR  ...
# 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
# 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
# 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
# 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68,
# 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85,
# 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 
# 99.
# 
# Done.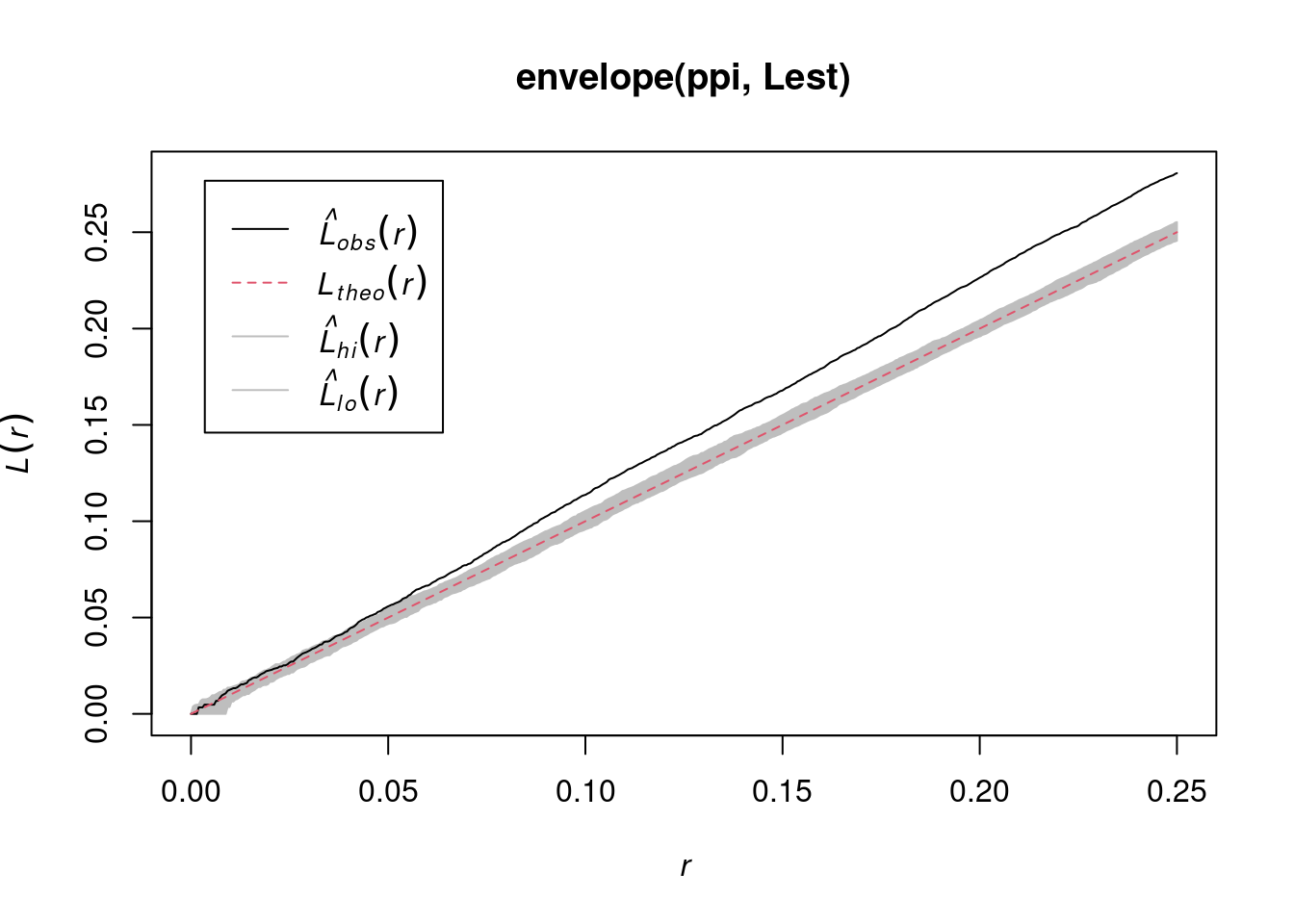

envelope(ppi, Linhom) |> plot()
# Generating 99 simulations of CSR  ...
# 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
# 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
# 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
# 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68,
# 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85,
# 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 
# 99.
# 
# Done.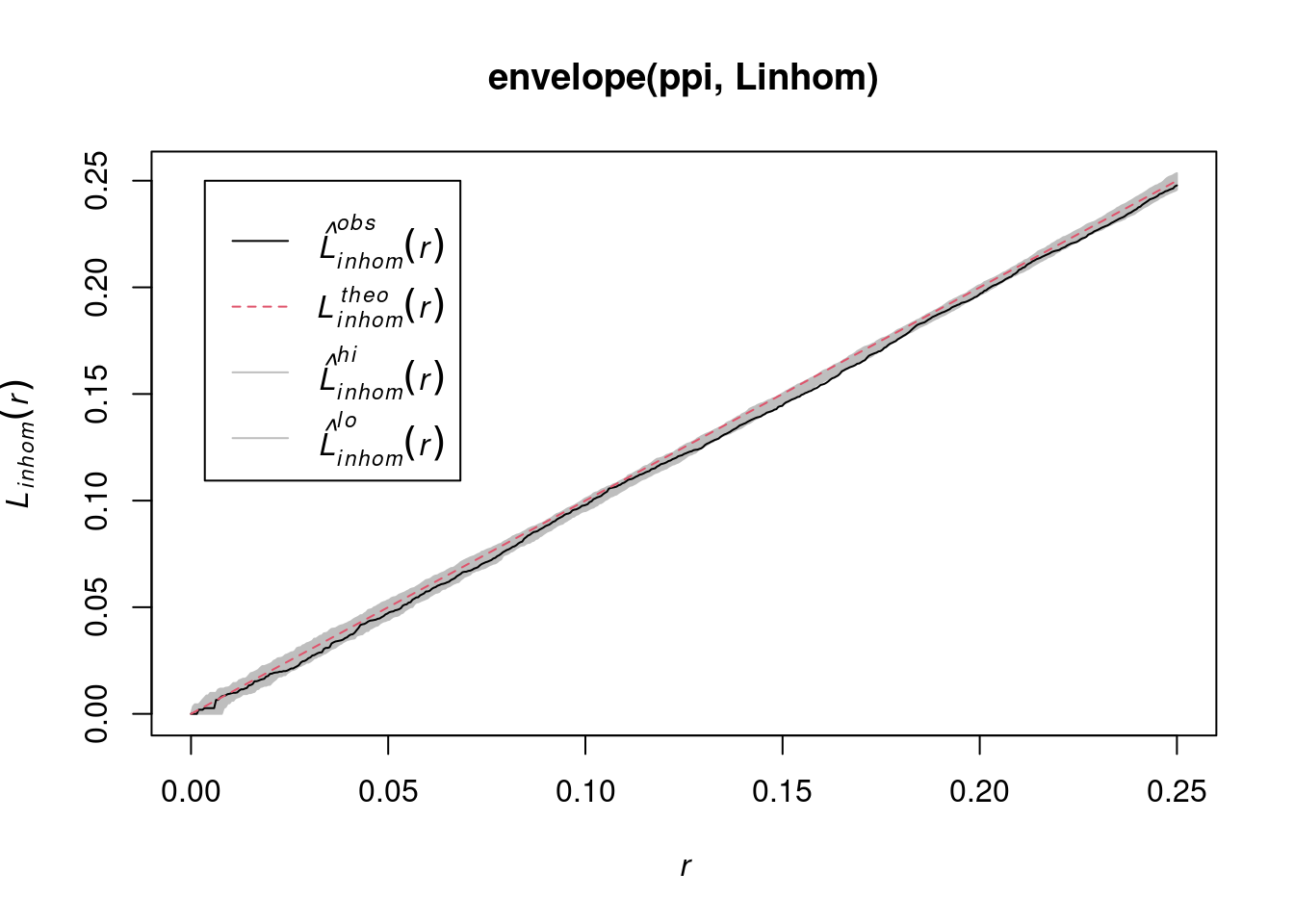

envelope(Y , Lest) |> plot()
# Generating 99 simulations of CSR  ...
# 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
# 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
# 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
# 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68,
# 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85,
# 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 
# 99.
# 
# Done.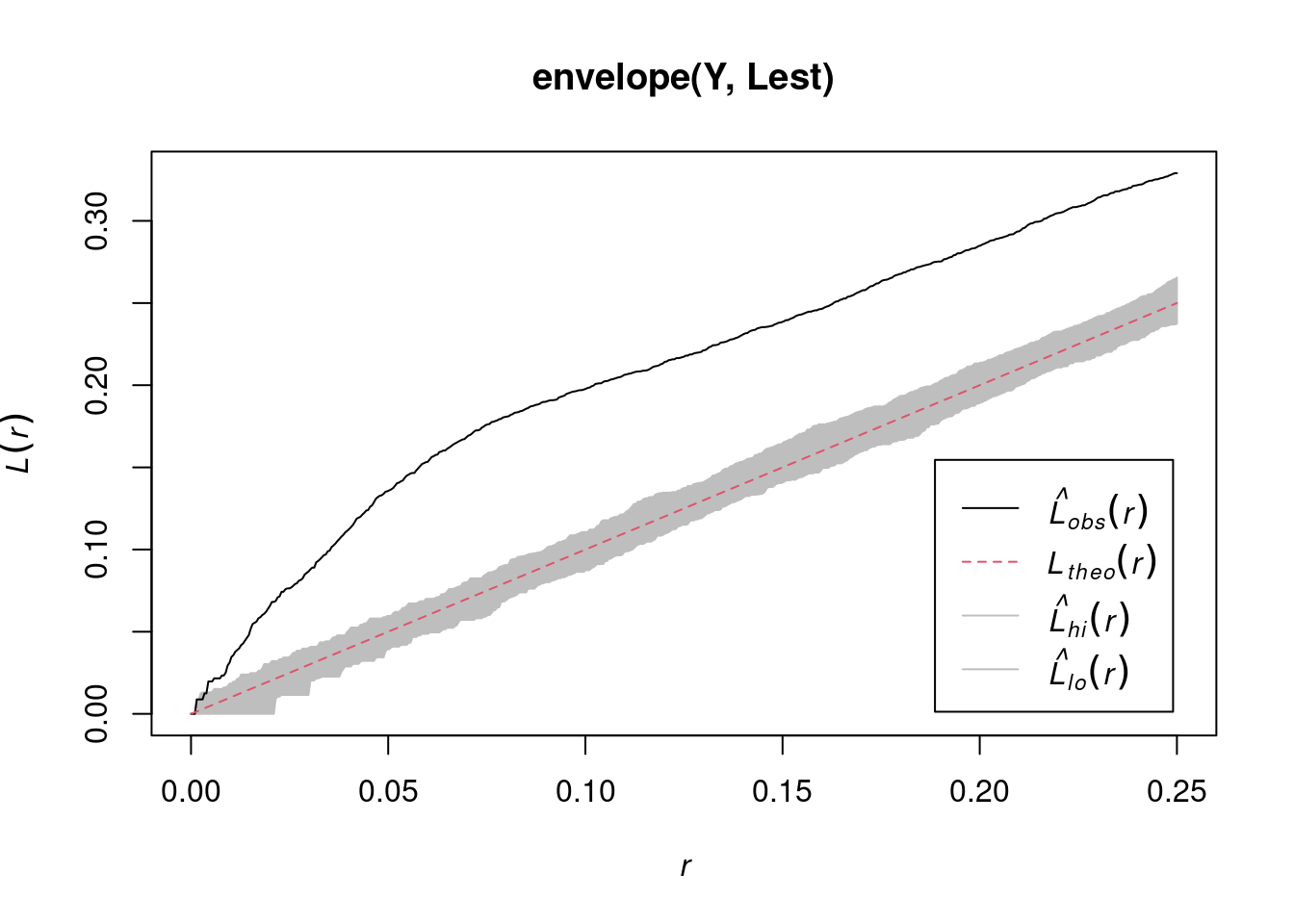

envelope(Y , Linhom) |> plot()
# Generating 99 simulations of CSR  ...
# 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
# 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
# 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
# 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68,
# 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85,
# 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 
# 99.
# 
# Done.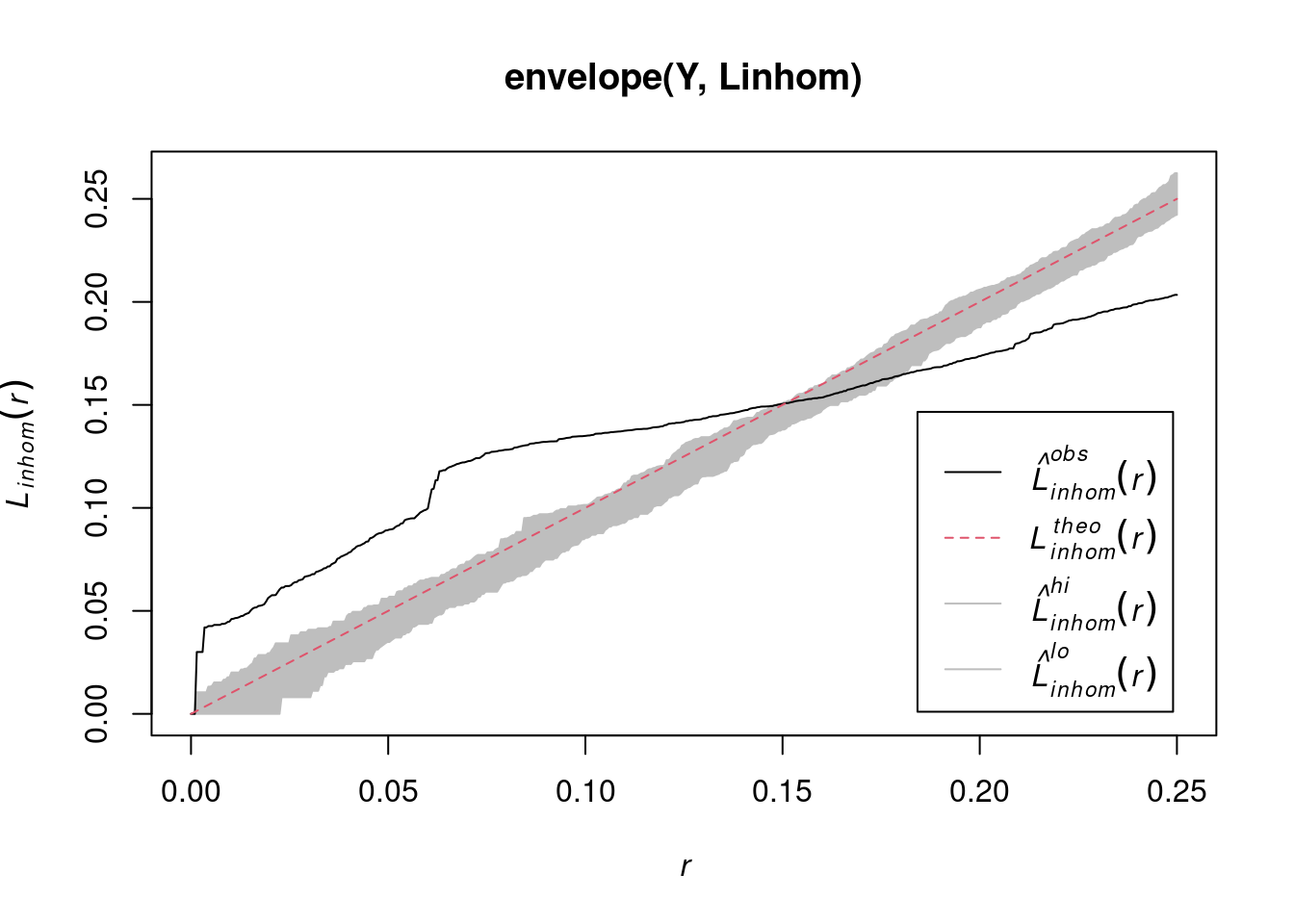

2.8 Fitting models to clustered data

# assuming Inhomogeneous Poisson:
ppm(ppi, ~x)
# Nonstationary Poisson process
# Fitted to point pattern dataset 'ppi'
# 
# Log intensity:  ~x
# 
# Fitted trend coefficients:
# (Intercept)           x 
#        4.33        1.96 
# 
#             Estimate  S.E. CI95.lo CI95.hi Ztest  Zval
# (Intercept)     4.33 0.174    3.99    4.67   *** 24.91
# x               1.96 0.247    1.48    2.45   ***  7.96
# assuming Inhomogeneous clustered:
kppm(Y, ~x)
# Inhomogeneous cluster point process model
# Fitted to point pattern dataset 'Y'
# Fitted by minimum contrast
#   Summary statistic: inhomogeneous K-function
# 
# Log intensity:  ~x
# 
# Fitted trend coefficients:
# (Intercept)           x 
#        3.69        1.47 
# 
# Cluster model: Thomas process
# Fitted cluster parameters:
# kappa scale 
# 7.731 0.038 
# Mean cluster size:  [pixel image]
# 
# Cluster strength: phi =  7.122
# Sibling probability: psib =  0.8769

2.9 MaxEnt and species distribution modelling

It seems that MaxEnt fits an inhomogeneous Poisson process

Starting from presence (only) observations, it

adds background (absence) points, uniformly in space
fits logistic regression models to the 0/1 data, using environmental covariates
ignores spatial interactions, spatial distances

R package maxnet does that using glmnet (lasso or elasticnet regularization on)

A maxnet example using stars is available in the development version, which can be installed directly from github by remotes::install_github("mrmaxent/maxnet") ; and the same maxnet example using terra (thanks to Ben Tupper).

Relevant papers:

a paper detailing the equivalence and differences between point pattern models and MaxEnt is found here.
A statistical explanation of MaxEnt for Ecologists

2.10 Exercises

From the point pattern shown in section 1.3, download the data as GeoPackage, and read into R
Read the boundary of Germany using rnaturalearth::ne_countries(scale = "large", country = "Germany")
Create a plot showing both the observation window and the point pattern
Do all observations fall inside the observation window?
Create a ppp object from the points and the window
Create a density map of the wind turbines, with the turbines added
Test whether the point pattern is homogeneous
Create a plot with the (estimated) density of the wind turbines, with the turbine points added
Verify that the mean density multiplied by the area of the window approximates the number of turbines
Test for interaction: create diagnostic plots to verify whether the point pattern is clustered, or exhibits repulsion

2.11 Further reading

E. Pebesma, 2018. Simple Features for R: Standardized Support for Spatial Vector Data. The R Journal 10:1, 439-446.
A. Baddeley, E. Rubak and R Turner, 2016. Spatial Point Patterns: methodology and Applications in R; Chapman and Hall/CRC 810 pages.
J. Illian, A. Penttinen, H. Stoyan and D. Stoyan, 2008. Statistical Analysis and Modelling of Spatial Point Patterns; Wiley, 534 pages.

Learning goals

Reading materials

2.1 Intro to sf and stars

Why do all functions in sf start with st_?

The larger geospatial open source ecosystem

sf operators, how to understand?

2.2 sf and spatstat

Why is this important?

2.3 Exercises

2.4 Intro to spatstat

2.5 Checking homogeneity

2.6 Estimating density

2.7 Assessing interactions: clustering/inhibition

2.8 Fitting models to clustered data

2.9 MaxEnt and species distribution modelling

2.10 Exercises

2.11 Further reading

2.1 Intro to `sf` and `stars`

Why do all functions in `sf` start with `st_`?

`sf` operators, how to understand?

2.2 `sf` and `spatstat`

2.4 Intro to `spatstat`