7  Unknown, constant mean

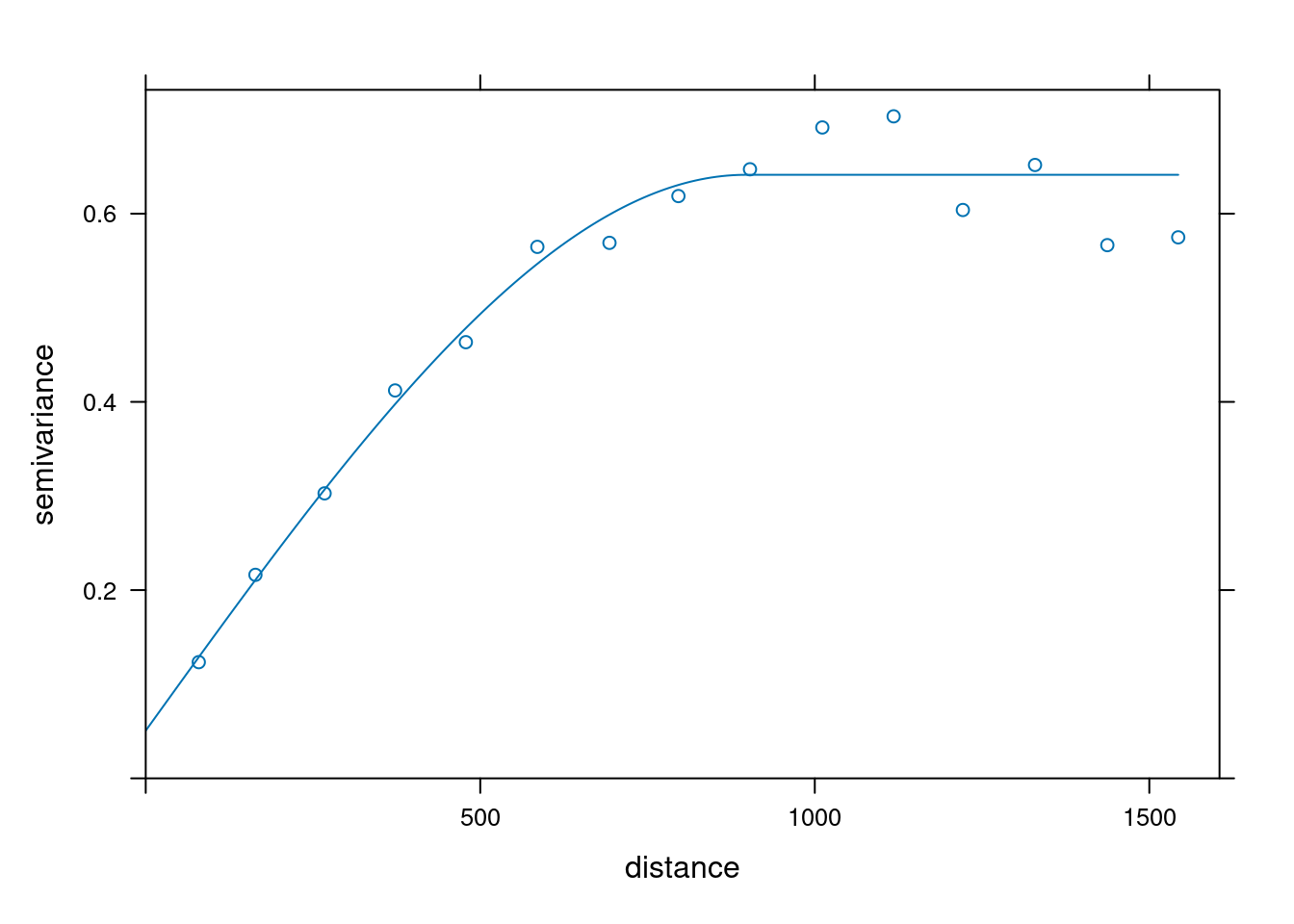
\[ \newcommand{\E}{{\rm E}} % E expectation operator \newcommand{\Var}{{\rm Var}} % Var variance operator \newcommand{\Cov}{{\rm Cov}} % Cov covariance operator \newcommand{\Cor}{{\rm Corr}} \]

Suppose the mean is constant, but not known. This is the most simple realistic scenario. We can estimate it from the data, taking into account their covariance (i.e., using weighted averaging):

\[\hat{m} = ({\bf 1}'V^{-1}{\bf 1})^{-1} {\bf 1}'V^{-1}Z\] with \({\bf 1}\) a conforming vector with ones, and substitute this mean in the SK prediction equations: BLUP/Ordinary kriging: \[\hat{Z}(s_0) = \hat{m} + v'V^{-1} (Z-\hat{m})\] \[\sigma^2(s_0) = \sigma^2_0 - v'V^{-1}v + Q\] with \(Q = (1 - {\bf 1}'V^{-1}v)'({\bf 1}'V^{-1}{\bf 1})^{-1}(1 - {\bf 1}'V^{-1}v)\)

Stationarity 1

Given prediction location \(s_0\), and data locations \(s_1\) and \(s_2\), we need: \(\Var(Z(s_0))\), \(\Var(Z(s_1))\), \(\Var(Z(s_2))\), \(\Cov(Z(s_0),Z(s_1))\), \(\Cov(Z(s_0),Z(s_2))\), \(\Cov(Z(s_1),Z(s_2))\).

How to get these covariances?

  • given a single measurement \(z(s_1)\), we can not infer \(\Var(Z(s_1))\)
  • given two measurements \(z(s_1)\) and \(z(s_2)\), we can never infer \(\Cov(Z(s_1),Z(s_2))\)
  • geven a time series at \(s_1\) and \(s_2\), we can infer
    • \(\Cov(Z(s_1),Z(s_2))\), but how to infer
    • \(\Cov(Z(s_0),Z(s_1))\) and
    • \(\Cov(Z(s_0),Z(s_2))\)?

Solution: assume stationarity.

Stationarity 2

Stationarity of the

  • mean \(\E(Z(s_1)) = \E(Z(s_2)) = ... = m\)
  • variance \(\Var(Z(s_1)) = \Var(Z(s_2)) = ... = \sigma^2_0\)
  • covariance \(\Cov(Z(s_1),Z(s_2)) = \Cov(Z(s_3),Z(s_4))\) if \(s_1-s_2=s_3-s_4\): distance/direction dependence

Second order stationarity: \(\Cov(Z(s),Z(s+h)) = C(h)\)

which implies: \(\Cov(Z(s),Z(s)) = \Var(Z(s))= C(0)\)

The function \(C(h)\) is the covariogram of the random function \(Z(s)\)

From covariance to semivariance

Covariance: \(\Cov(Z(s),Z(s+h)) = C(h) = \E[(Z(s)-m)(Z(s+h)-m)]\)

Semivariance: \(\gamma(h) = \frac{1}{2} \E[(Z(s)-Z(s+h))^2]\)

\(\E[(Z(s)-Z(s+h))^2] = \E[(Z(s))^2 + (Z(s+h))^2 -2Z(s)Z(s+h)]\)

\(\E[(Z(s)-Z(s+h))^2] = \E[(Z(s))^2] + \E[(Z(s+h))^2] - 2\E[Z(s)Z(s+h)] = 2\Var(Z(s)) - 2\Cov(Z(s),Z(s+h)) = 2C(0)-2C(h)\)

\(\gamma(h) = C(0)-C(h)\)

\(\gamma(h)\) is the semivariogram of \(Z(s)\).

The Variogram

library(sf)
data(meuse, package = "sp")
meuse = st_as_sf(meuse, coords = c("x", "y"))
library(gstat)
v = variogram(log(zinc) ~ 1, meuse)
v.fit = fit.variogram(v, vgm(1, "Sph", 900, 1))
plot(v, v.fit)

The Variogram

  • the central tool to geostatistics
  • like a mean squares (variance) in analysis of variance, like a \(t\) to a \(t\)-test
  • measures spatial correlation
  • subject to debate: it involves modelling
  • synonymous to semivariogram, but
  • semivariance is not synonymous to variance

Variogram: how to compute

average squared differences: \[\hat{\gamma}(\tilde{h})=\frac{1}{2N_h}\sum_{i=1}^{N_h}(Z(s_i)-Z(s_i+h))^2 \ \ h \in \tilde{h}\]

  • divide by \(2N_h\):
    • if finite, \(\gamma(\infty)=\sigma^2\)
    • semi variance
  • if data are not gridded, group \(N_h\) pairs \(s_i,s_i+h\) for which \(h \in \tilde{h}\), \(\tilde{h}=[h_1,h_2]\)
  • choose about 10-25 distance intervals \(\tilde{h}\), from length 0 to about on third of the area size
  • plot \(\gamma\) against \(\tilde{h}\) taken as the average value of all \(h \in \tilde{h}\)

Variogram: terminology

plot(v, v.fit)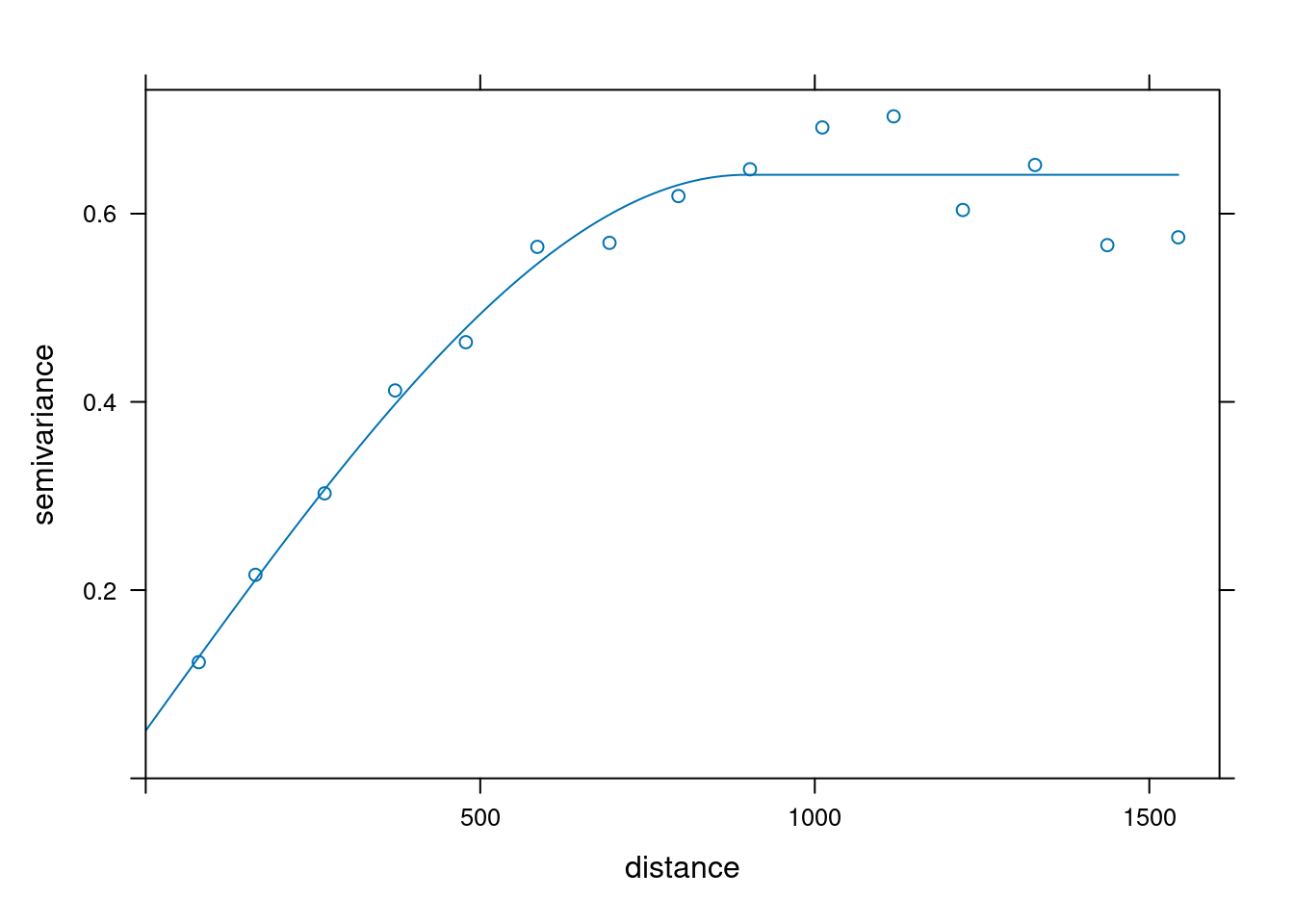

v.fit
#   model  psill range
# 1   Nug 0.0507     0
# 2   Sph 0.5906   897
vgm(psill = 0.6, model = "Sph", range = 900, nugget = 0.06)
#   model psill range
# 1   Nug  0.06     0
# 2   Sph  0.60   900

or simpler, with un-named arguments: ::: {.cell}

vgm(0.6, "Sph", 900, 0.06)
#   model psill range
# 1   Nug  0.06     0
# 2   Sph  0.60   900

:::

Why prefer the variogram over the covariogram

Covariance: \(\Cov(Z(s),Z(s+h)) = C(h) = \E[(Z(s)-m)(Z(s+h)-m)]\)

Semivariance: \(\gamma(h) = \frac{1}{2} \E[(Z(s)-Z(s+h))^2]\)

\[\gamma(h)=C(0)-C(h)\]

  • tradition
  • \(C(h)\) needs (an estimate of) \(m\), \(\gamma(h)\) does not
  • \(C(0)\) may not exist (\(\infty\)!), when \(\gamma(h)\) does (e.g., Brownian motion)

Known, varying mean

This is nothing else then simple kriging, except that the mean is no longer constant; BLP/Simple kriging: \[\hat{Z}(s_0) = \mu(s_0) + v'V^{-1} (Z-\mu(s))\] \[\sigma^2(s_0) = \sigma^2_0 - v'V^{-1}v\] with \(\mu(s) = (\mu(s_1),\mu(s_2),...,\mu(s_n))'\).